
Constantemente encontramos distintas formas a nuestro alrededor, tanto en la naturaleza como
en las obras humanas, y es la geometría —una de las ramas más antiguas de las matemáticas
— la que estudia dichas formas. Algunos de los fenómenos cotidianos que desde la infancia
nos despiertan la curiosidad son, sin duda, las formas esféricas de las burbujas de jabón
flotando en las plazas públicas. Todo niño (o adulto) se emociona al sumergir aros circulares de
alambre en agua jabonosa para obtener una película más o menos plana, si lo logramos, se
nos dibuja una amplia sonrisa y vemos el goce que experimentan al soplar a través de dicha
película para formar esferas casi perfectas que se mantienen por cierto tiempo volando en el
aire.
Una pregunta que surge de inmediato, aunque quizás no todos la hayan notado, es ¿Por
qué las formas obtenidas son esferas? Pareciera que es por la forma circular del aro, pero
un poco de experimentación deformando dicho arco, puede convencernos de que esa no es la
causa. Experimentado un poco más, empleando varios aros deformados entrelazados de
distintas formas, se pueden obtener diferentes formas empleando películas jabonosas. Te
proponemos que hagas lo siguiente:
Experimento
En una primera etapa tomamos dos aros circulares de radios idénticos R contenidos en
planos paralelos, manteniendo una distancia relativamente pequeña entre ellos y cuidando que
el eje de los centros se mantenga en una recta perpendicular a los planos de los aros.
Introducimos los aros en jabón con agua, tratando de formar una sola película jabonosa cuyo
borde consta de ambos aros. ¿Qué forma tiene?
Si no hiciste el experimento, quizás pienses que se forma un cilindro, pero la observación
nos convence de que más bien la película jabonosa adopta la forma de una superficie
«curvada». Es un ejemplo de una superficie de revolución, la cual es ampliamente conocida
por los alfareros de Capula quienes saben que, al hacer girar un torno, y proponiendo un
«perfil» adecuado, se obtiene una vasija con una forma específica. En nuestro caso, dicho perfil
está descrito por una curva especial llamada catenaria, por eso la superficie de revolución de
nuestro interés se llama catenoide. El nombre de catenaria obedece a la forma que adopta una
cadena colgando de dos extremos, un cable de luz sostenido por dos postes, o en general
cualquier objeto homogéneo pesado que tiene un largo excepcionalmente grande, respecto a
sus otras dimensiones.
En una segunda etapa del experimento, una vez que formamos la película jabonosa con
forma de catenoide, separamos lentamente los planos de dichos aros. Aumentando esta
distancia, que denotamos h, y manteniendo el eje de los centros perpendiculares a los planos
de los aros, se obtienen superficies cada vez más esbeltas. En efecto, el radio del cuello de la
catenoide, que denotamos a, se hace cada vez más pequeño, hasta que la catenoide
finalmente se rompe. Este fenómeno es abrupto y produce un cambio de forma. Así, a una
distancia crítica constante h_c, ya no hay catenoide, sino que esta se rompe y se forman dos
discos separados rellenando el interior de cada uno de los aros. El lector, que por flojera de
hacer el experimento quisiera adivinar qué es lo que ocurre, quizás pensaría que el cuello de la
superficie tiende a hacerse cada vez más pequeño hasta llegar a a = 0, colapsando

la superficie como el vértice de un cono, separándose enseguida en dos discos rellenando los
aros. La observación, sin embargo, no sustenta ese experimento mental. Lo que ocurre en la
realidad, es que el cuello de la catenoide ciertamente se hace pequeño, pero no llega a ser
cero. Más bien a una separación específica de los aros se produce la ruptura de forma abrupta.
¿Cómo explicar este proceso discontinuo de cambio de forma?
En el primer caso, una superficie curva que evoluciona conforme separamos los aros, se
rompe y luego se convierte en dos superficies planas (el interior de los aros circulares) en el
segundo caso. La rama de las matemáticas que resuelve este tipo de problemas se llama
Cálculo de Variaciones, materia que se aborda en algunos cursos avanzados de física como
mecánica clásica; en economía aparece con el nombre de optimización dinámica; y en
ingenierías como control óptimo. Históricamente, el Cálculo de Variaciones se desarrolló un
poco después del Cálculo Diferencial e Integral, el cual se estudia ampliamente en
bachillerato y en las ingenierías. En geometría, muchos problemas acerca de los volúmenes
contenidos por burbujas fueron matemáticamente estudiados, empleando esta herramienta
desde el siglo XIX. En ese entonces, se demostró por primera vez que la esfera era la mejor
manera de contener un volumen dado con una superficie de jabón. Dicho resultado fue
conjeturado dos mil años antes por matemáticos griegos. Desde entonces, se han obtenido
resultados a distintos problemas acerca de burbujas de jabón. En la década de 1990, por
ejemplo, se resolvió un problema difícil que describe cómo contener dos volúmenes de aire con
burbujas de jabón. El mismo problema para tres volúmenes ha tenido avances importantes solo
hasta la década de 2020.
De acuerdo al Cálculo de Variaciones, para un borde de alambre fijo de todas las posibles
superficies que tienen dicho borde, las películas de jabón adoptan la forma de la superficie que
tiene el área mínima, denotamos dicha área por S. En geometría se les llama superficies
mínimas. Así la catenoide es un ejemplo de superficie mínima.
Explicación
El Cálculo de Variaciones da cuenta de lo que ocurre en nuestro experimento. Para
separaciones pequeñas h, hay dos posibles soluciones de superficies que minimizan el área
contenida entre ambos aros, las cuales se llaman soluciones críticas y las dos son
catenoides. Una de esas soluciones es la solución «real» que físicamente podemos
observar, la otra es una solución «virtual» que aparece por la forma de las ecuaciones
que resultan. En la siguiente figura, mostramos dos catenarias correspondiendo a los perfiles
de las catenoides, una virtual y otra real. Al hacer crecer h, la forma de la catenoide «real» se
va modificando de tal manera que el radio del cuello a de la superficie, obedece
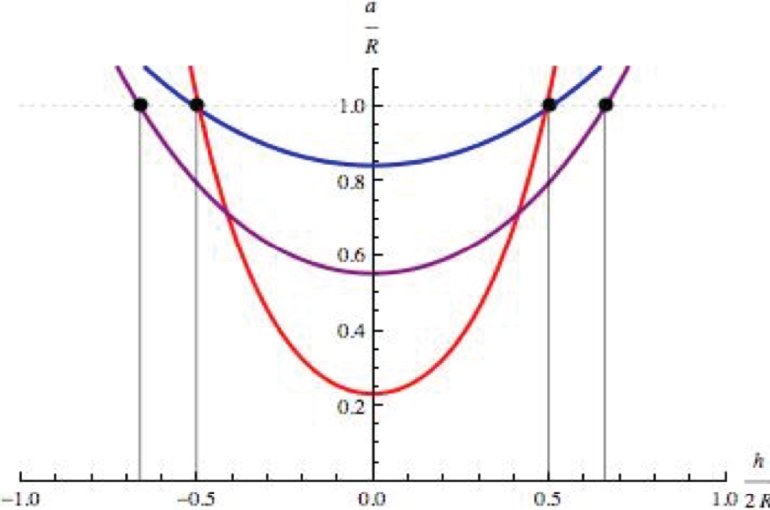

una relación específica que depende de h. Por otro lado, la catenoide «virtual» va incrementando el radio de su cuello.
En un valor específico tendremos:
h_c / R = 1.3254; a_c / R = 0.55243
Ambas catenarias, la «real» y la «virtual», son una misma. En ese instante se produce la
ruptura que da lugar a dos discos de radio R. Como cada disco tiene área 3.1416 R, entonces
ambos discos bordean un área total de S = 6.2832 R^2. En la siguiente figura se muestran
datos experimentales contrastados con la relación teórica entre h y a. El valor de ruptura
experimental coincide con el valor predicho h_c / R = 1.33.
Un hecho notable predicho por la teoría y confirmado por el experimento, es una transición
‘abrupta’ en la que la superficie de área mínima va incrementando continuamente su área S al
hacer crecer h, hasta alcanzar la distancia crítica h_c. Para dicha distancia crítica, el área de la
catenoide alcanza el valor S = 7.53781 R^2. Inmediatamente después de la ruptura, el área
disminuye de manera discontinua hasta el área de los dos discos, S = 6.2832 R^2.
El Cálculo de Variaciones tiene múltiples aplicaciones en problemas de optimización
en economía y finanzas, por ejemplo, para tomar en cuenta las distintas restricciones que el
mercado impone sobre la evolución del precio de un bien, para lo cual emplean métodos de
optimización dinámica. En la ingeniería, el control óptimo de sistemas se emplea en el
diseño de robots, en diseño de reacciones químicas, en sistemas de potencias, etc.; también se
emplean las herramientas del cálculo de variaciones. Sin mencionar la importancia central que
tiene el llamado principio de mínima acción en el desarrollo de la física experimental de
partículas y la fundamentación epistemológica del llamado modelo estándar.
Homero G. Díaz-Marín. Profesor Investigador de la Facultad de Ciencias Físico-
Matemáticas. Universidad Michoacana de San Nicolás de Hidalgo. Morelia, Michoacán.
Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Osvaldo Osuna-Castro. Profesor Investigador del Instituto de Física y Matemáticas.
Universidad Michoacana de San Nicolás de Hidalgo. Morelia, Michoacán.
Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Masato I. y Taku S. (2010). In situ observation of a soap–film catenoid–a simple educational physics
experiment. Eur. J. Phys, (31), 357-365. https://doi.org/10.1088/0143-0807/31/2/013
Matson J. (2013). La evolución de las espumas. Investigación y Ciencia, 446 (Noviembre), 6-7.
https://www.investigacionyciencia.es/revistas/investigacion-y-ciencia/alimentacin-587/la-evolucin-de-las-
espumas-11515
