No te preocupes, si continúas leyendo te darás cuenta que estás obedeciendo a uno de los principios más importantes en la física: el principio de mínima acción.
Los físicos somos personas muy curiosas a las que nos gusta observar y analizar la naturaleza. Entre otras cosas, queremos comprender los fenómenos que suceden a nuestro alrededor y para ello empleamos un lenguaje especial y abstracto llamado matemáticas.
Formulación de las leyes de Newton
Para entender el movimiento de los cuerpos usamos la mecánica, es decir, la rama de la física que se encarga de estudiar a los objetos en reposo o en movimiento. Con ella, una vez que se conoce la posición inicial, la velocidad inicial y las fuerzas que actúan sobre dichos objetos, tenemos el conocimiento completo de cómo se moverán en el espacio. Decimos entonces que se conoce la dinámica del sistema y sabemos en dónde estará y cómo se moverá el objeto en todo momento.
Esta formulación se la debemos al físico, matemático, filósofo, teólogo y alquimista inglés Isaac Newton, quien fue capaz de demostrar que las leyes que gobiernan la caída de las manzanas en la tierra, son las mismas que originan el movimiento de los planetas. Podemos enunciar las tres leyes que rigen el comportamiento mecánico de los cuerpos (leyes de Newton) de la siguiente forma:
- Ley de la inercia: Todo cuerpo en reposo o en movimiento a lo largo de una línea recta con velocidad constante permanecerá en el mismo estado físico, a menos que se le apliquen fuerzas externas.
- Ley de las fuerzas: La aceleración que actúa sobre un cuerpo está dada por la suma de las fuerzas que actúan sobre él, es decir, fuerza es igual a masa por aceleración.
- Ley de acción-reacción: Cuando aplicamos una fuerza sobre un objeto aparece una fuerza de reacción con la misma intensidad pero en sentido contrario.
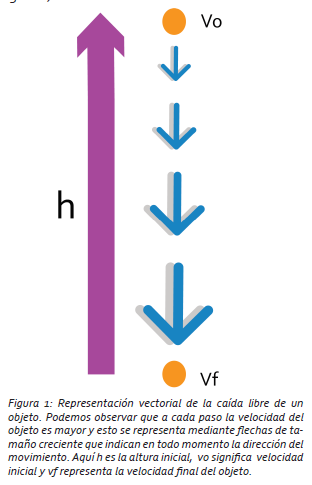
Todo lo anterior se denomina análisis vectorial de la naturaleza, ya que todas las que variables con las que trabajamos están dadas por medio de vectores. Estos son objetos matemáticos que se usan para representar la posición, la velocidad y la aceleración que tienen los cuerpos por medio de una cantidad que posee una magnitud (un número), una dirección y un sentido (figura 1).
Aun cuando el análisis mediante vectores es completo y permite predecir la evolución de los sistemas físicos, en muchas ocasiones es difícil encontrar las ecuaciones de movimiento por medio del análisis vectorial. Lo que es peor, puede suceder que aun cuando sea posible escribir dichas ecuaciones, no existan soluciones que puedan ser obtenidas haciendo los cálculos con lápiz y papel. En este punto es necesario hacer uso de las computadoras e intentar hallar soluciones de manera aproximada usando programas de cálculo numérico.
Para evitar estos problemas algunos físicos idearon una nueva forma de estudiar a la naturaleza usando la ley de la conservación de la energía, la cual como su nombre indica, nos dice que la energía no se crea ni se destruye, sino que se transforma.
La naturaleza y el gasto mínimo de energía
Las primeras ideas en cuanto a la forma económica en que actúa la naturaleza fueron propuestas por el abogado y matemático francés, Pierre de Fermat en el año de 1662. Fermat consideraba que los rayos de luz que viajan de un punto a otro lo hacen por medio del camino por el cual lleva menos tiempo realizar el recorrido. Años más tarde, en 1774 el filósofo, matemático y astrónomo francés Pierre Louis Maupertuis, estipuló que la naturaleza actúa siempre “gastando” la menor cantidad de energía posible.
Para entender mejor estas ideas vamos a imaginar que se deja caer un objeto desde la azotea de un edificio:
¿Qué trayectoria crees que seguirá?
¿Caerá en línea recta o hará una o más curvas en el aire antes de llegar al suelo?
La experiencia nos dice que la primera opción es la correcta y esto se debe a que la distancia más corta entre dos puntos es la línea recta. Esto implica menor tiempo de recorrido y nos recuerda la idea de Fermat.
Por otro lado:
¿Te has dado cuenta que cada vez que se forman burbujas son siempre esféricas?
¿Por qué no hay burbujas en forma de cubos o de pirámides?
Esto se debe a que la figura geométrica de superficie más pequeña que es capaz de contener un mayor volumen de aire, es la esfera (figura 2). En éstas podemos ver que se está economizando (por decirlo de algún modo) en el material de construcción, lo cual nos recuerda a su vez la idea de Maupertius.
Ley de la conservación de la energía
Según la física, cuando hablamos de energía nos referimos a la propiedad que poseen todos los objetos en el universo de producir un trabajo. Otra forma de ver a la energía es mediante sus manifestaciones en forma de luz, calor, o como en el caso de la mecánica, por medio de lo que llamamos energía cinética y energía potencial. La energía cinética existe únicamente cuando los objetos se encuentran en movimiento, es decir, un objeto en reposo no posee energía cinética.
La energía cinética depende de la velocidad a la que el objeto se está moviendo de manera que, mientras más rápido se mueva, mayor energía cinética posee. Por otro lado, la energía potencial aparece cuando se somete al objeto a la influencia de una o varias fuerzas. Para entender mejor esto vamos a tomar como ejemplo la caída de los cuerpos bajo la influencia de la gravedad de la Tierra.
Cuando levantamos un objeto en presencia de la fuerza de la gravedad, éste adquiere energía potencial, al soltarlo comienza a caer con una velocidad cada vez mayor hasta alcanzar un valor máximo un instante antes de tocar el suelo. Conforme la velocidad aumenta también aumenta la energía cinética, caso contrario a la energía potencial, la cual disminuye ya que la altura es cada vez menor. Se dice entonces que la energía potencial se transforma en energía cinética, y si la suma de ambas energías no cambia en el tiempo se tiene que la energía mecánica total se conserva.
Mecánica analítica
Como vimos anteriormente, cuando sumamos la energía cinética y la energía potencial, obtenemos la energía total de un objeto.
Ahora bien:
¿Qué sucede si tomamos la diferencia?
¿De alguna manera será algo útil para explicar el comportamiento de la naturaleza?
Esta interrogante llevó en 1778 al físico, matemático y astrónomo franco-italiano Joseph Louis de Lagrange, a reescribir la mecánica de Newton a partir de un objeto matemático al que llamó Lagrangiano. Éste se define como la diferencia entre la energía cinética y la energía potencial y dio origen a una nueva forma de estudiar a la mecánica llamada mecánica analítica.
Entre sus principales propiedades se tiene la de simplificar las ecuaciones de movimiento, facilita los cálculos y permite obtener de forma directa leyes de conservación. Además, define a una cantidad llamada acción, la cual puede entenderse como el producto de la energía empleada en llevar a cabo un proceso por el tiempo que tarda en realizarse.
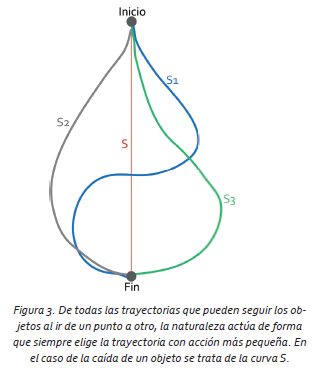
Vamos a usar de nuevo el ejemplo de la caída libre de un cuerpo para explicar cómo funciona el principio de mínima acción. Imaginemos un cuerpo que cae, pero nosotros no sabemos de qué forma lo hace. En principio, existen infinitas trayectorias que el objeto podría seguir en su viaje desde la posición inicial hasta el suelo. Lo que sí podemos decir es cómo se comportan la energía cinética y potencial en cada una de las trayectorias.
Construyendo el Lagrangiano de cada camino y obteniendo la acción en cada caso, observamos que la trayectoria que ocurre en el mundo real es la que tiene la acción más pequeña de todas (figura 3). Es decir, lo que nos dice el principio de mínima acción es que siempre la naturaleza actúa de forma que su evolución se presenta a través del camino que minimiza a la acción.
Aun cuando los ejemplos que hemos visto están definidos en el contexto de la física clásica, es importante mencionar que el principio de mínima acción también es válido en el marco de la física moderna, como es el caso de la relatividad general[1] y de las teorías clásicas de campo[2]. Desafortunadamente, cuando nos referimos al estudio de situaciones de la mecánica cuántica[3], esto ya no es válido, debido a que se presentan fenómenos que, entre otras cosas ya no cumplen con nuestra idea de un sólo camino permitido.
Es necesario entonces definir herramientas más sofisticadas para llevar a cabo un estudio similar al que hemos presentado.
Saber más
Feynman et al. 2006. Las lecturas de física. Addison Wesley.
http://www.feynmanlectures.caltech.edu/I_toc.html
Penrose. 2007. El camino a la realidad. Vintage books.
Viniegra-Herbelín. 2011. Una mecánica sin talachas. Fondo de cultura económica.
https://fisicaiteb.files.wordpress.com/2014/08/37220088-una-mecanica-sin-talachas.pdf
El Dr. Roberto De Arcia es egresado el Instituto de Física y Matemáticas de la Universidad Michoacana de San Nicolás de Hidalgo y actualmente se encuentra realizando una estancia postdoctoral en la Universidad de Guanajuato.
[1] La relatividad general es la teoría con la que los físicos estudiamos a la fuerza de gravedad. Nos dice que todos los objetos del universo que poseen materia y energía son capaces de curvar al espacio que está alrededor de ellos, y es justamente esta curvatura lo que experimentamos como gravedad.
[2] La teoría clásica de campos permite estudiar la interacción entre las partículas a través del concepto de campo de fuerzas. Esto es una región del espacio capaz de generar fuerzas sobre los objetos y se usa comúnmente para explicar, entre otras cosas, a fenómenos de tipo gravitacional o electromagnético.
[3] La mecánica cuántica es la teoría que describe el mundo microscópico y permite entre otras cosas explicar la estructura atómica y describir la interacción entre las partículas. Su origen proviene de la imposibilidad de trabajar fenómenos microscópicos usando la física clásica.