En la Edad Media, la cultura en Europa fue obstruida severamente, hasta el Renacimiento, cuando los logros de épocas anteriores fueron redescubiertos. En particular, esto incluyó a las matemáticas que se desarrollaron en Grecia antigua. Posteriormente, los renacentistas quisieron avanzar más allá de este conocimiento. Un tema clave, que fascinó a una generación de eruditos, fue la búsqueda de las raíces de los polinomios cúbicos. Aquí revisamos la dramática historia de su solución, que fue un acto simbólico para abrir el camino a un mayor progreso – y una revolución verdadera – en matemáticas, ciencia y tecnología, con un enorme impacto sobre generaciones futuras, hasta el día de hoy.

En el Renacimiento tardío, durante el siglo XVI, el norte de Italia era centro de la cultura europea. Esto incluyó campos como la pintura, la literatura, la arquitectura y también las matemáticas, en las que la Universidad de Bolonia tuvo un papel dominante. El conocimiento de Grecia antiguafue difundido entre los académicos, en particular a través del libro “Elementos” de Euclides y las habilidades matemáticas ganaron importancia práctica en la economía.

Tales aplicaciones requirieron de cálculos cada vez más avanzados, además de conocimiento teórico en aritmética. En este sentido, usualmente el objetivo es encontrar soluciones a alguna ecuación. El tipo más simple y obvio de ecuación es de la forma polinomial, a₀ + a₁x + a₂x² + ... + a_nxⁿ = 0, donde las a_i representan constantes. Estas ecuaciones polinomiales tienen un número enorme de aplicaciones en toda clase de contextos. El reto es encontrar las raíces de estos polinomios, es decir, los valores de la variable x que satisfacen la ecuación. La dificultad para hacerlo depende principalmente del grado del polinomio, es decir, de la potencia máxima n que aparece. La solución a la ecuación lineal (n=1), a₀ + a₁x = 0, es evidente; para n=2, a₀ + a₁ x + a₂ x² = 0, aún es sencillo resolverla, su solución era conocida en Grecia antigua[1] y ahora es cotidiana en las escuelas secundarias. La idea es eliminar el término lineal, a₁x, a través de la sustitución y = x+a₁ / (2a²).

Más allá, para n>2, la tarea se vuelve mucho más difícil. El truco mostrado aún se puede aplicar para eliminar el término x^n–1, pero esto ya no resuelve el problema. Este enigma había atraído el interés de los antiguos babilonios y egipcios. Los antiguos griegos estaban interesados en el caso n=3, la ecuación cúbica, en particular Diofanto, Hipócrates y Arquímedes, pero fallaron al resolverlo (salvo casos específicos). En el siglo VII, el matemático y astrónomo chino Wang Xiaotong resolvió otro conjunto de ecuaciones cúbicas específicas.

La búsqueda de una solución general fue un reto simbólico y práctico para los matemáticos renacentistas en un intento no solo para entender matemáticas antiguas, sino para ir más allá y adquirir conocimiento nuevo.

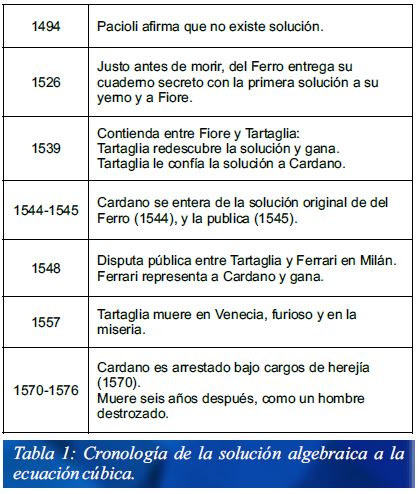
En 1494, Luca Pacioli, profesor en Bolonia, escribió su libro[2] “Summa de Arithmetica”, donde presentaba el problema, y arguyó que no hay soluciones generales para n>2. Estaba equivocado, pero su intuición fue correcta en que solo existen soluciones algebraicas generales, en términos de raíces de números, hasta cierto valor máximo de n, que de hecho es n=4 –esto se estableció en el siglo XIX como el Teorema de Abel-Ruffini. En particular, Pacioli no sabía que una solución para la ecuación cúbica, con n=3, ya se había encontrado – al menos geométricamente – cuatro siglos antes.

Solución geométrica en Persia medieval

Durante la congelación cultural en Europa medieval, aún había trabajo matemático siendo realizado en el mundo islámico. El astrónomo, filósofo, poeta y matemático persa Omar Khayyám (1048-1131), que vivió en las ciudades de Nishpur, Samarkand y Bukhara, fue una personalidad muy destacada. Concibió la construcción de un observatorio astronómico y diseñó un calendario solar de precisión sorprendente, que es la base del calendario iraní actual.

Khayyám fue también el primero en encontrar una solución geométrica a la ecuación cúbica (sin el término cuadrático, a₂=0), que presentó en su libro “Tratado sobre las Demostraciones de Problemas de Álgebra” (reproducimos su solución en la parte A del Suplemento de este artículo que aparece en  http://www.sabermas.umich.mx/docs/suplemento_a.pdf). Ese libro también contiene el arreglo triangular de los coeficientes binomiales, que ahora es conocido como triángulo de Pascal – hoy en día es familiar para los estudiantes de bachillerato.

Solución algebraica en Italia renacentista

Regresamos a Bolonia: en forma algebraica, Scipione del Ferro (1465-1526) fue el primero en resolver la ecuación x³ + a₁x + a₀ = 0, suponiendo a las constantes a₀ y a₁ como positivas – en ese tiempo, todavía no se usaban números negativos. Nunca publicó su solución, pero la escribió en un cuaderno secreto, que dio en su lecho de muerte a su yerno y a un estudiante llamado Antonio Maria Fiore. Este último lo usó en 1535 para retar al matemático veneciano Niccolò Tartaglia en una contienda pública. Estas contiendas eran comunes en esa época: dos matemáticos se entregaban el uno al otro un compendio de unos 30 problemas y después de aproximadamente un mes evaluaban cuántos problemas había resuelto el oponente. El ganador recibía dinero o una comida lujosa para toda su familia y, particularmente, reconocimiento y posibilidades de un ascenso, mientras que el perdedor estaba en peligro de perder su empleo y sus fondos.

Todos los problemas de Fiore eran del tipo que del Ferro dominaba. Tartaglia descubrió la solución independientemente y resolvió todos los problemas matemáticos de Fiore, en tanto que Fiore no pudo resolver ninguno de los de Tartaglia.

La vida trágica de Niccolò Tartaglia comenzó en 1499 o 1500 en Brescia, Italia. Su padre, cartero a caballo, fue asesinado en 1505. En 1512 su ciudad natal fue invadida por soldados franceses, después de resistir un cerco durante una semana. Los franceses cometieron una masacre terrible, asesinando a más de 45,000 residentes. Un soldado cortó el mentón y el paladar de Niccolò con un sable. Como consecuencia, solo pudo tartamudear durante mucho tiempo. Este fue el origen de su apodo Tartaglia (“tartamudo”), que mantuvo durante toda su vida, aunque aparentemente recobró un habla fluida de adulto – no se conoce con seguridad su apellido real. Posteriormente, escondió sus cicatrices tras una barba tupida.

A los 14 años, Niccolò asistió a una escuela donde le enseñaban las letras en orden alfabético. Sin embargo, al llegar a la letra K ya no pudo pagar la cuota. Entonces, aprendió las demás letras de forma autodidacta, junto con las matemáticas, a través de trabajo arduo, que él llamó la “hija de la pobreza”.

Su extraordinaria habilidad matemática le permitió ganarse la vida mediante cálculos mercantiles y como maestro privado. Tradujo el libro “Elementos” al italiano, y en 1548-1549 dio un curso sobre ese libro en la Universidad de Brescia, pero nunca recibió el salario que se le había prometido. A pesar de ser uno de los matemáticos más destacados de su época, pasó toda su vida en pobreza.

Tartaglia comprendió como lidiar con la ecuación cúbica (sin el término cuadrático, a₂x²) el 12 de febrero de 1539, lo que le permitió resolver los 30 problemas de Fiore en dos horas. También mantuvo en secreto su solución, como lo hizo antes del Ferro. Hubo razones para ello en vista de nuevas contiendas matemáticas; él tenía claro que podrían ser cruciales para obtener empleos e ingresos.

Sin embargo, un médico milanés, llamado Cardano, expresó gran interés en su solución. Después de insistir varias veces, Tartaglia le confió la solución, codificada en un poema, bajo la condición de un juramento que obligaba a Cardano a no revelarla nunca a nadie, pues juró “por la biblia y por su honor”. Ahora ya no es un secreto, así que describimos su solución (en notación moderna) en la parte B del Suplemento de este artículo que aparece en http://www.sabermas.umich.mx/docs/suplemento_b.pdf.

Girolamo Cardano tenía casi la misma edad que Tartaglia; nació en 1501 en Milán, como hijo (ilegítimo) de un abogado, que era amigo de Leonardo da Vinci. Cardano fue uno de los últimos sabios universales verdaderos. Durante su larga vida (hasta 1576) escribió más de 200 libros o artículos sobre medi­ci­na (que estudió en Padua), matemáticas, filosofía, teología, astronomía (aún no bien separada de la astrología), arquitectura, historia, física (electricidad y magnetismo, hidrodinámica), química, ingeniería (¡su eje de transmisión aún es conocido en la mecánica!), e interpretación de los sueños. Era admirado por su extenso conocimiento, pero también odiado por su lengua afilada y aseveraciones críticas, que incluso llevaron a intentos de asesinarlo. Su vida estuvo llena de aventuras, entre la pobreza y la prosperidad. En su época, fue conocido principalmente como un médico exitoso, pionero en la investigación sobre la tifoidea, tuberculosis, asma, sífilis y gonorrea (fue el primero en distinguir las últimas dos). Sus terapias eran adelantadas a su tiempo y pudo salvar las vidas de algunos pacientes, incluyendo al arzobispo escocés, que había sido desauciado por otros médicos. Recibió ofertas para ser médico personal de VIPs[3] de toda Europa, las cuales rechazó. En 1570, tuvo que pasar varios meses en prisión por acusaciones de herejía.

En cuanto a las matemáticas, descubrió las reglas de la teoría de probabilidad combinatoria que usó para ganar dinero en juegos de azar (en los que participaba casi a diario)[4]. Esto se explica en su libro “Liber de ludo aleae”, junto con métodos eficientes de hacer trampa.

Se podría pensar que todos estos logros son más que suficientes para una sola persona; pero además, en 1545, publicó su libro controversial “Ars magnae Regulis Algebraicis”. Este escrito presentaba las soluciones generales para ecuaciones polinomiales de tercer y cuarto orden. Así, contenía la solución de Tartaglia, por lo que había roto su juramento de mantenerla en secreto. Su justificación fue que ya no se sintió ligado por su juramento tras saber que Scipione del Ferro la había descubierto antes que Tartaglia. De hecho, durante un viaje a Bolonia en 1544, el yerno de del Ferro le había mostrado el cuaderno secreto con la solución original. En su libro, Cardano le dio parte del crédito a Tartaglia. Aún así, no sorprendentemente, Tartaglia estaba lleno de ira: un año después publicó su libro “Quesiti et invenzioni diverse” donde tachaba a Cardano de mentiroso y plagiario, además de tonto, incapaz de resolver incluso un problema simple.

La polémica consecuente fue muy amarga, pero ahora es una excelente fuente de información para los historiadores. La posición de Cardano fue defendida por su brillante estudiante Lodovico Ferrari, a quien Cardano había adoptado cuando era un huérfano pobre. Después del intercambio de varios panfletos públicos (“cartelli”), hubo una confrontación final: una disputa pública entre Tartaglia y Ferrari (Cardano rechazó participar) en Milán, el 10 de agosto de 1548, cerca del lugar donde posteriormente se construyó la famosa casa de ópera Teatro alla Scala. Tartaglia era el más experimentado, pero las habilidades en retórica y matemáticas de Ferrari eran superiores, por lo que tenía a la mayoría de la audiencia a su favor. Preguntó sarcásticamente por qué Tartaglia no permitía la publicación del descubrimiento de del Ferro.

El debate debía continuar el día siguiente, pero Tartaglia sintió que las cosas iban mal para él. Esa noche huyó de Milán, habiendo perdido su prestigio y su ingreso (entonces ocurrió que la Universidad de Brescia se negó a pagar su salario). Además, fue condenado a retirar sus acusaciones contra Cardano. Aunado a esa decisión cuestionable, hasta el día de hoy dicha solución es conocida como la “Fórmula de Cardano”.[5] Tartaglia murió 9 años después en Venecia.

Con todo esto, de hecho es correcto que Cardano había generalizado la solución a las ecuaciones cúbicas. La restricción a coeficientes positivos marcaba la distinción en múltiples casos (dependiendo de en que lado de la ecuación se colocaba un término); del Ferro y Tartaglia solo manejaron parte de estos casos.[6] Esto parecía natural en el contexto de la imagen geométrica, donde la ecuación significa la comparación de volúmenes. Cardano fue el primero en incluir en sus cálculos números negativos que denotó como “ficticios”. Notó que podían ser usados igual que los números positivos, lo que le permitió resolver todos los casos a la vez. Además, en su discusión también introdujo soluciones imaginarias – en el sentido de que supuso la existencia de raíces cuadradas de números negativos – pero no comprendía las propiedades de los números complejos. Es sorprendente que hayan aparecido por primera vez en ese contexto, y no como solución de ecuaciones cuadráticas. Lo último habría sido más obvio desde el punto de vista mo­der­no, pero, por supuesto, los números negativos son un pre-requisito. Así, Cardano hizo contribuciones relevantes en este tema, aunque no en honestidad.

Para la solución de la ecuación de un polinomio de grado n=4 (a través de la reducción a uno cúbico), dio todo el crédito a su estudiante Ferrari, quien sucedió a Cardano en su prestigioso puesto universitario, aunque solo tenía 18 años cuando Cardano se retiró.[7]

Epílogo

Después de todo, en el marco de esta disputa trágica, se logró un descubrimiento impresionante, posiblemente el primer paso sustancial de las matemáticas europeas más allá del conocimiento de Grecia antigua. La ecuación cúbica fue de importancia simbólica. Junto con la solución de la ecuación de cuarto grado, también dada en el libro de Cardano “Ars magnae”, el conjunto de raíces polinomiales en términos algebraicos ya estaba completo, de acuerdo con el Teorema de Abel-Ruffini, mencionado antes.[8]

Sin embargo, la novedad más poderosa fue el resultado de familiarizarse con los números negativos,[9] y algunas ideas iniciales sobre los números complejos.[10] Esto tiene un enorme impacto en la ciencia y tecnología, hasta el día de hoy, y es enseñado regularmente en bachillerato (a diferencia de la solución de la ecuación cúbica). Así, ha cambiado el mundo y nuestra forma de pensar, y los acontecimientos detrás son verdaderamente memorables.

Y una última lección a ser aprendida: si descubres algo importante, no lo dudes: ¡ve y publícalo!

“Dr. Wolfgang Bietenholz es investigador del Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de México y el Lic. Héctor Mejía-Díaz es estudiante de maestría.”

 

---

[1] Aquí escribimos las ecuaciones polinomiales en nuestra notación moderna. En el mundo antiguo no se expresaban así, ni tampoco en el Renacimiento. Usualmente, la gente se refería a una imagen geométrica, lo que explica por qué el uso de números negativos no era evidente para ellos.

[2] Una manera eficiente de imprenta era conocida en Europa desde el siglo XV, lo que fue otro avance en comparación con la cultura antigua (sin saber que había sido descubierta en China, siglos antes).

[3] Del inglés “Very Important Person”, que en español significa “persona muy importante”.

[4] Un siglo después estas reglas fueron redescubiertas y extendidas en Francia, particularmente por Blaise Pascal y Pierre de Fermat.

[5] Al menos existe una ecuación conocida como “Fórmula de Tartaglia”: expresa el vo­lu­men de un tetraedro, como una generalización tridimensional de la Fórmula de Herón para el área de un triángulo.

[6] En su interpretación geométrica, cada término de la ecuación cúbica representaba el volumen de un cuboide (que tiene forma de una caja de zapatos), y se tenía que encontrar una longitud lateral x tal que dos sumas de volúmenes fueran iguales. Por lo tanto suponían que cada término era positivo; entonces, por ejemplo, consideraban a, x³ + a₁x + a₀ = 0 o x³ + a₁ x = a₀ o x³+ a₀ = a₁x o x³ = a₁x + a₀, como cuatro ecuaciones diferentes. La inclusión del término a₂ x² conducía a más casos aún.

[7] Mientras que Cardano podía estar orgulloso de su hijo adoptivo, Ferrari, fue menos afortunado con sus propios hijos: su hija Chiara murió de sífilis (y Cardano cínicamente usó su caso para sus estudios médicos). Aparentemente, su hijo Giovanni envenenó a su esposa – por lo que fue condenado y ejecutado. Su segundo hijo, Aldo, tuvo una fuerte disputa con su padre, quien lo desheredó. Tras una carrera criminal y estancias en al menos ocho prisiones, se convirtió en torturador y verdugo de la inquisición, y estuvo involucrado en los cargos de herejía contra su padre. Cuando Cardano fue liberado (gracias al apoyo del arzobispo de Edimburgo, a quién él había salvado), estaba en un estado patético y se le prohibió enseñar o publicar por el resto de su vida.

[8] Por supuesto, ahora las raíces de polinomios mayores se pueden encontrar numéricamente. El número de éstas (contado con la multiplicidad) es siempre n, según el Teorema Fundamental del Álgebra.

[9] Es posible que no todos estén completamente felices con este adelanto, insistiendo en que sin la noción de números negativos, el concepto de deuda no existiría.

[10] La primera discusión sobre números complejos apareció en 1572, en un libro de Rafael Bombelli, el último gran matemático renacentista de Bolonia. Sin embargo, solo desde el siglo XVIII se han aceptado y usado generalmente estos números en matemáticas.

{jcomments on}