Page 27 - No_73
P. 27
Año 13 /Enero -Febrero/ No. 73 U.M.S.N.H.
la superficie como el vértice de un cono, separán- dos mil años antes por matemáticos griegos. Des-
dose enseguida en dos discos rellenando los aros. de entonces, se han obtenido resultados a distintos
La observación, sin embargo, no sustenta ese ex- problemas acerca de burbujas de jabón. En la déca-
perimento mental. Lo que ocurre en la realidad, es da de 1990, por ejemplo, se resolvió un problema
que el cuello de la catenoide ciertamente se hace difícil que describe cómo contener dos volúmenes
pequeño, pero no llega a ser cero. Más bien a una de aire con burbujas de jabón. El mismo problema
separación específica de los aros se produce la rup- para tres volúmenes ha tenido avances importan-
tura de forma abrupta. tes solo hasta la década de 2020.
De acuerdo al Cálculo de Variaciones, para un
¿Cómo explicar este proceso discontinuo de cam- borde de alambre fijo de todas las posibles superfi-
bio de forma? cies que tienen dicho borde, las películas de jabón
En el primer caso, una superficie curva que adoptan la forma de la superficie que tiene el área
evoluciona conforme separamos los aros, se rom- mínima, denotamos dicha área por S. En geometría
pe y luego se convierte en dos superficies planas (el se les llama superficies mínimas. Así la catenoide es
interior de los aros circulares) en el segundo caso. un ejemplo de superficie mínima.
La rama de las matemáticas que resuelve este tipo
de problemas se llama Cálculo de Variaciones, ma- Explicación
teria que se aborda en algunos cursos avanzados El Cálculo de Variaciones da cuenta de lo que
de física como mecánica clásica; en economía apa- ocurre en nuestro experimento. Para separaciones
rece con el nombre de optimización dinámica; y en pequeñas h, hay dos posibles soluciones de superfi-
ingenierías como control óptimo. Históricamente, cies que minimizan el área contenida entre ambos
el Cálculo de Variaciones se desarrolló un poco aros, las cuales se llaman soluciones críticas y las
después del Cálculo Diferencial e Integral, el cual dos son catenoides. Una de esas soluciones es la
se estudia ampliamente en bachillerato y en las in- solución «real» que físicamente podemos obser-
genierías. En geometría, muchos problemas acerca var, la otra es una solución «virtual» que aparece
de los volúmenes contenidos por burbujas fueron por la forma de las ecuaciones que resultan. En
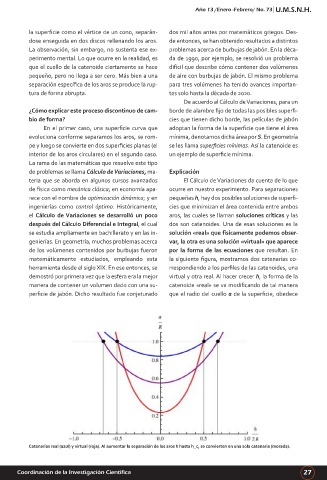
matemáticamente estudiados, empleando esta la siguiente figura, mostramos dos catenarias co-
herramienta desde el siglo XIX. En ese entonces, se rrespondiendo a los perfiles de las catenoides, una
demostró por primera vez que la esfera era la mejor virtual y otra real. Al hacer crecer h, la forma de la
manera de contener un volumen dado con una su- catenoide «real» se va modificando de tal manera
perficie de jabón. Dicho resultado fue conjeturado que el radio del cuello a de la superficie, obedece
Catenarias real (azul) y virtual (roja). Al aumentar la separación de los aros h hasta h_c, se convierten en una sola catenaria (morada).
Coordinación de la Investigación Científica 27